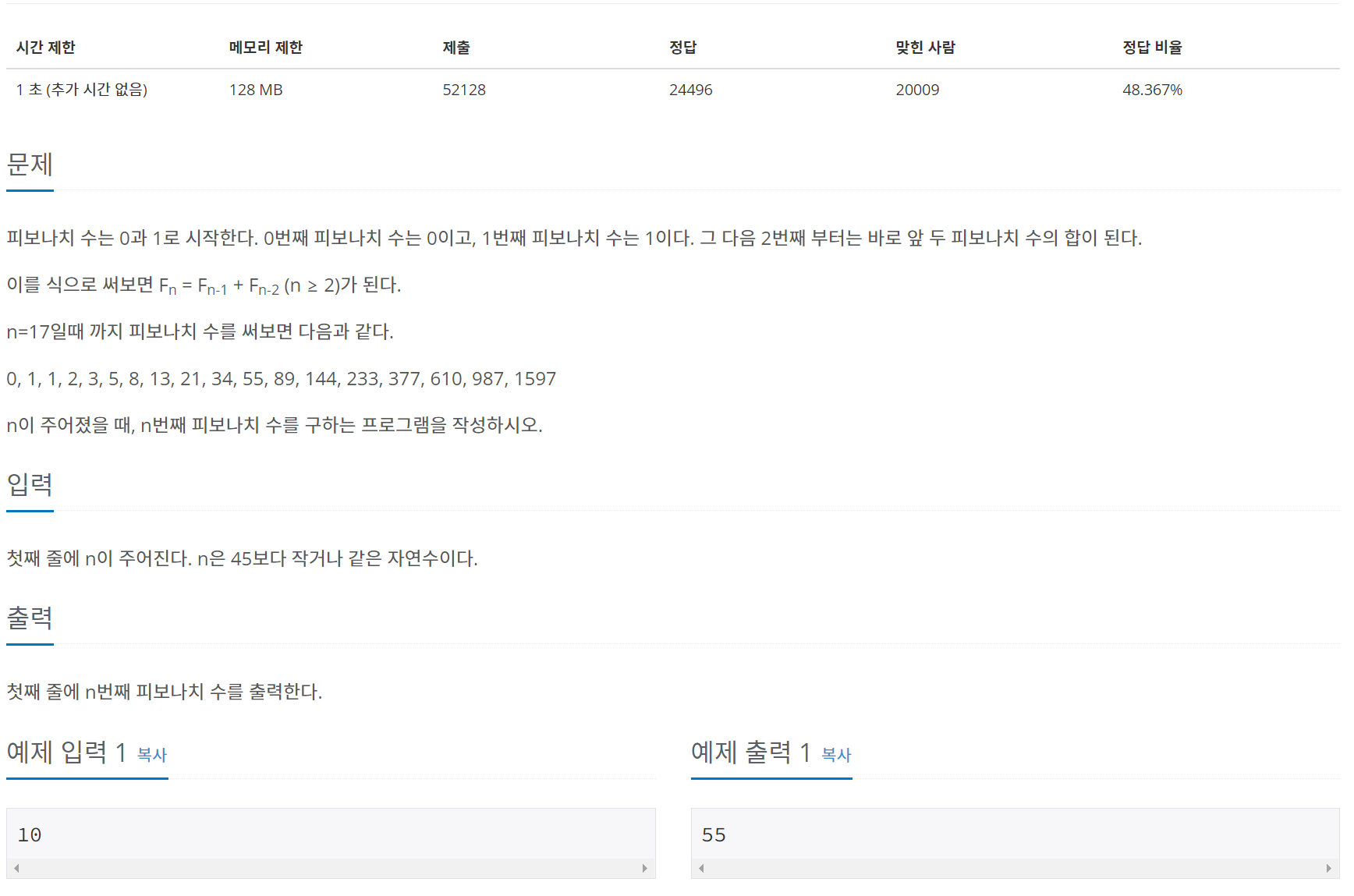
백준-2747. 피보나치 수1
카테고리 : Algorithm >> Dynamicprogramming
DP의 대표적인 문제로 “top-bottom”, “bottom-top”방식으로 다양하게 풀어보자.
- base check
- memoization
- recurrence relation
방식을 고려하면 풀어보았다.
C++ 코드
#include <iostream>
#include <algorithm>
using namespace std;
int d[50];
int dp(int n) {
//1. base check
if (n <= 1) return n;
//2. memoization
if (d[n] > 0) return d[n];
//3. recurrence relation
d[n] = dp(n - 1) + dp(n - 2);
return d[n];
}
int main() {
int N;
scanf("%d", &N);
printf("%d", dp(N));
}
C# 코드
using System;
namespace C_sharp_ex
{
class Program
{
static void Main(string[] args)
{
int N = int.Parse(Console.ReadLine());
int[] d = new int[50];
d[1] = 1;
for(int i = 2; i <= N; i++)
d[i] = d[i - 1] + d[i - 2];
Console.Write(d[N]);
}
}
}
Java 코드
import java.io.*;
import java.util.*;
public class Main {
static int[] d = new int[50];
public static int dp(int n){
//1. base check
if(n <= 1) return n;
//2. memoization
if(d[n] > 0) return d[n];
//3. recurrence relation
d[n] = dp(n-1) + dp(n-2);
return d[n];
}
public static void main(String[] args) throws IOException {
Scanner s = new Scanner(System.in);
int n = s.nextInt();
System.out.println(dp(n));
}
}
Kotlin 코드
import java.util.*
val d = IntArray(50, {0})
fun dp(n: Int):Int {
if(n <= 1) return n
if(d[n] > 0) return d[n]
d[n] = dp(n-1) + dp(n-2)
return d[n]
}
fun main(args: Array<String>) {
val s = Scanner(System.`in`)
val input = s.nextInt()
print("${dp(input)}")
}
Python 코드
N = int(input())
d = [0 for _ in range(50)]
d[1] = 1
for i in range(2, N+1):
d[i] = d[i-1] + d[i-2]
print(d[N])
#파이썬은 메모리 초과 문제로 "bottom - up" 방식으로 해결