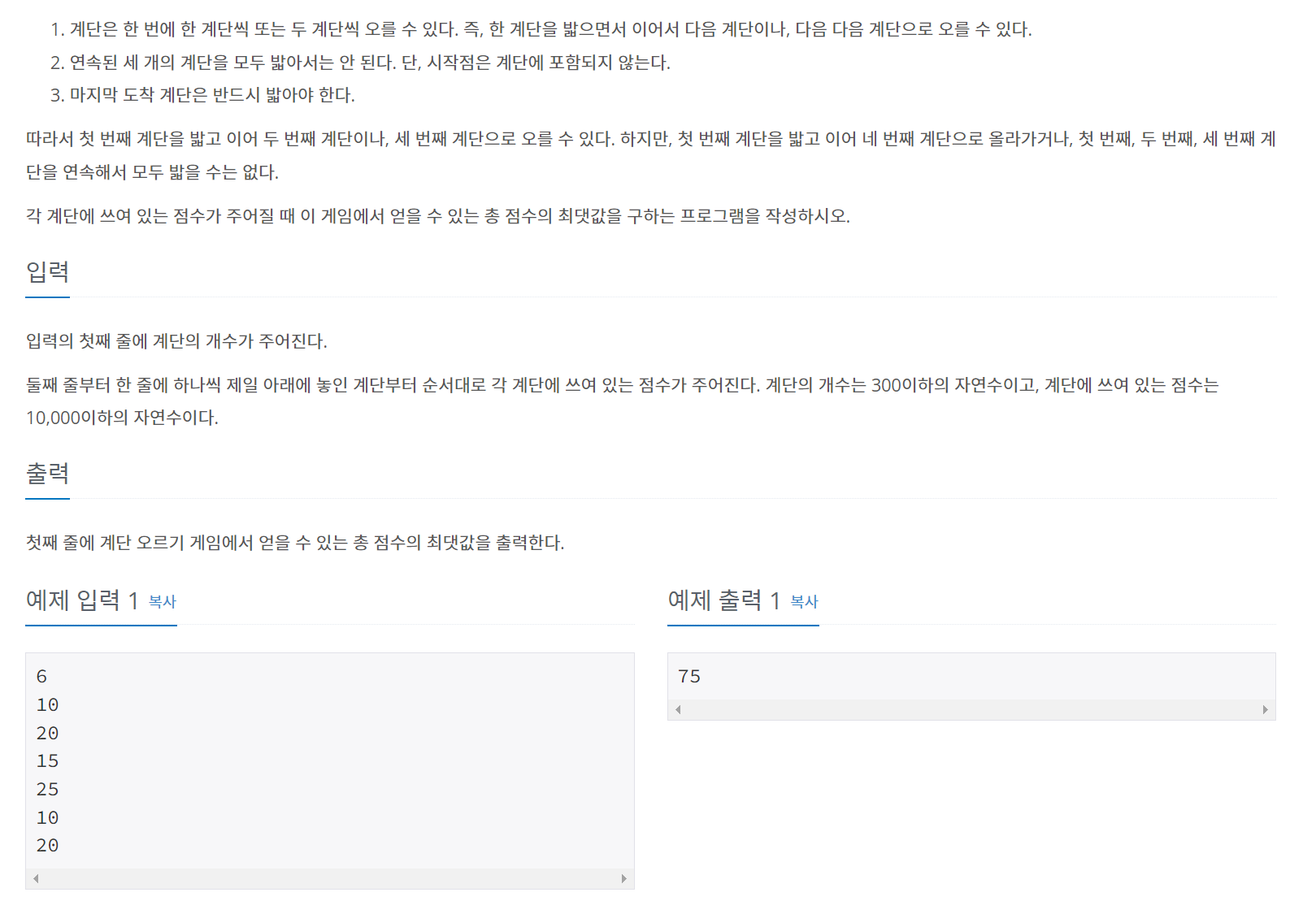
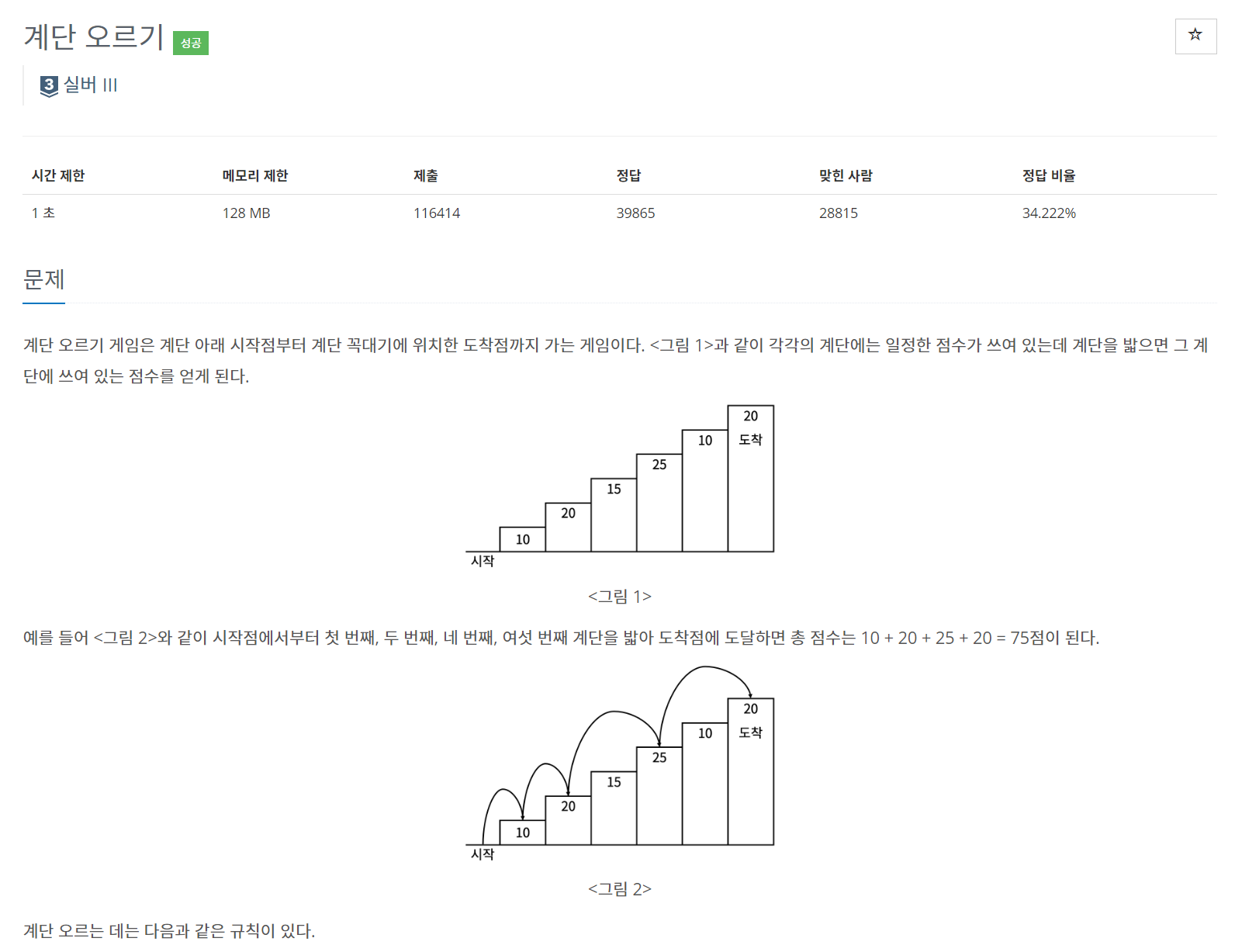
백준-2579. 계단 오르기
카테고리 : Algorithm >> Dynamicprogramming
- 2차원 다이나믹으로 풀이 a[n] : n번째 계단의 값.
d[n][t] : n번째 계단을 연속으로 t번째 밟은 경우의 최댓값.
이경우 여기선 연속으로 1번이나 2번 밟을 수 밖에없으므로, t는 1또는 2.
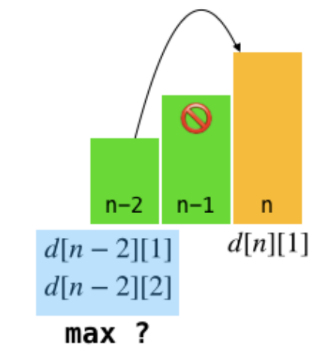
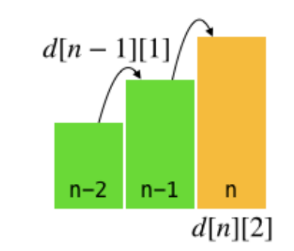
따라서, 우리가 구해야하는 d[n]은 d[n][1] 또는 d[n][2]중 더 큰 값이 되는것이다.
d[n][1] = max(d[n-2][1], d[n-1][2]) + a[n]
d[n][2] = d[n-1][1] + a[n]
따라서, 구하고자하는 점화식은 d[n] = max(d[n][1] , d[n][2]) 처음 1,2,3 계단은 앞의 경우가 없으므로 간단히 입력 후 시작.
1차원은 단순히 최댓값만 저장하는 방식이고, 2차원은 가능한 경우를 모두 저장한다는 방식의 차이 뿐이다.
C++ 코드(2차원 다이나믹/bottom-top)
#include <iostream>
using namespace std;
int d[301][3], a[301];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
d[0][1] = a[0];
d[1][1] = a[1];
d[1][2] = a[0] + a[1];
for (int i = 2; i < n; i++) {
d[i][1] = max(d[i - 2][1], d[i - 2][2]) + a[i];
d[i][2] = d[i - 1][1] + a[i];
}
cout << max(d[n - 1][1], d[n - 1][2]);
}
C++ 코드(1차원 다이나믹/bottom-top)
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
long arr[100] = { 0,1 };
int main() {
int n = 0;
scanf("%d", &n);
for (int i = 2; i <= n; i++) arr[i] = arr[i - 1] + arr[i - 2];
printf("%lld", arr[n]);
}
C++ 코드(top-bottom)
#include <iostream>
using namespace std;
int d[301], a[301];
int dp(int n) {
//base check
if (n == 0) return a[0];
else if (n == 1) return a[0] + a[1];
else if (n == 2) return max(a[0] + a[2], a[1] + a[2]);
//memoization
if (d[n] > 0) return d[n];
//recurence relation
int v = dp(n - 2) + a[n];
int k = dp(n - 3) + a[n - 1] + a[n];
d[n] = max(v, k);
return d[n];
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL);
int n;
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
cout << dp(n - 1);
}
C# 코드
using System.Text;
using System;
using static System.Console;
class Program
{
static int[] stairs = new int[302];
static int[] sum = new int[302];
public static void Main(string[] args)
{
int n = int.Parse(ReadLine());
for(int i =1; i <= n; i++)
{
stairs[i] = int.Parse(ReadLine());
}
sum[1] = stairs[1];
sum[2] = stairs[1] + stairs[2];
sum[3] = Math.Max(stairs[1], stairs[2]) + stairs[3];
for(int i = 4; i <= n; i++)
{
sum[i] = Math.Max(sum[i - 3] + stairs[i - 1], sum[i - 2]) + stairs[i];
}
Write(sum[n]);
}
}
Java 코드
import java.util.*;
public class Main {
static long[] stairs = new long[302];
static long[] sum = new long[302];
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int n = s.nextInt();
for(int i = 1; i <= n; i++){
stairs[i] = s.nextInt();
}
sum[1] = stairs[1];
sum[2] = stairs[1] + stairs[2];
sum[3] = Math.max(stairs[1], stairs[2]) + stairs[3];
for(int i = 4; i<=n; i++){
sum[i] = Math.max(sum[i-3] + stairs[i-1], sum[i-2]) + stairs[i];
}
System.out.println(sum[n]);
}
}
Kotlin 코드
import java.util.*
import kotlin.math.*
fun main(args: Array<String>){
val stairs = IntArray(302)
val sum = IntArray(302)
val s = Scanner(System.`in`)
val n = s.nextInt()
for(i in 1..n){
stairs[i] = s.nextInt()
}
sum[1] = stairs[1]
sum[2] = stairs[1] + stairs[2]
sum[3] = Math.max(stairs[1], stairs[2])+ stairs[3]
for(i in 4..n){
sum[i] = Math.max(sum[i-3]+stairs[i-1], sum[i-2])+stairs[i]
}
print(sum[n])
}
Python 코드
stairs = [0 for _ in range(302)]
sum = [0 for _ in range(302)]
n = int(input())
for i in range(1, n+1):
stairs[i] = int(input())
sum[1] = stairs[1]
sum[2] = stairs[1] + stairs[2]
sum[3] = max(stairs[1], stairs[2]) + stairs[3]
for i in range(4, n+1):
sum[i] = max(sum[i-3] + stairs[i-1], sum[i-2]) + stairs[i]
print(sum[n])